Dominando los sistemas de ecuaciones lineales: métodos y clasificación

Este método emplea la estrategia de multiplicar las ecuaciones por números específicos de modo que, al sumarlas, una de las dos incógnitas se elimine. Es ideal para casos donde las incógnitas tienen coeficientes similares, reduciendo el sistema a una ecuación lineal manejable.

Este método ofrece una ruta clara hacia la solución al despejar una de las incógnitas de una ecuación y sustituirla en la otra ecuación. Su simplicidad lo hace adecuado en diversas situaciones, independientemente de los coeficientes presentes.

Se despeja la misma incógnita en ambas ecuaciones y se igualan las expresiones obtenidas, encontrándose así la armonía entre ellas. Este método es especialmente útil cuando las incógnitas están despejadas de manera similar.

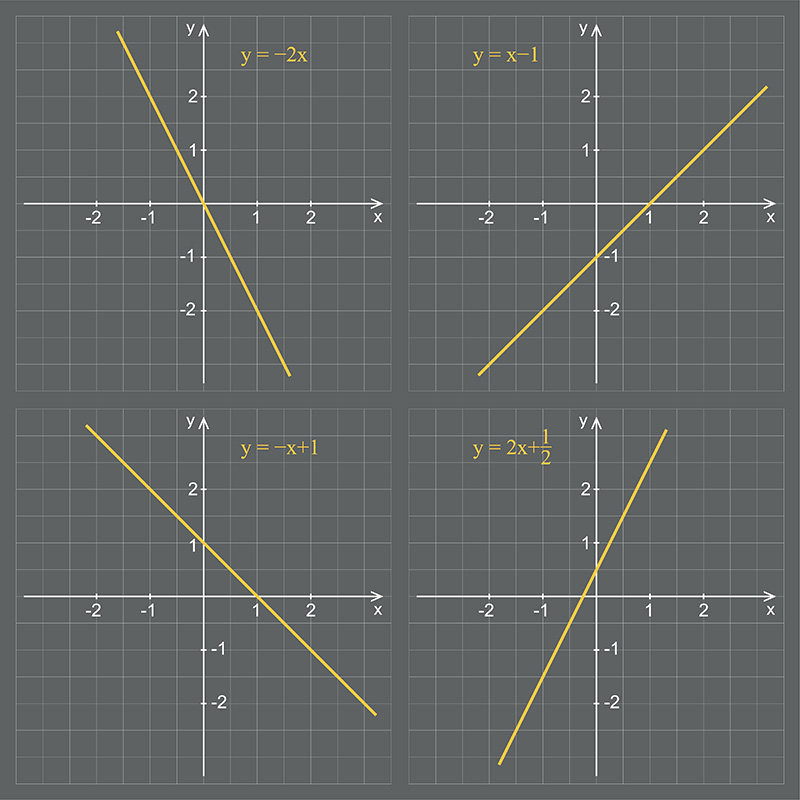
Se representan las ecuaciones del sistema sobre los ejes cartesianos. La intersección de los dos gráficos revela las soluciones. Es el método más apropiado para alumnos con habilidades espaciales.

Es importante recordar que, independientemente del método elegido, la solución siempre será la misma. Se recomienda encarecidamente verificar que las soluciones obtenidas cumplan con las ecuaciones originales.

Para comprender a qué tipo de sistema nos enfrentamos, es esencial realizar esta clasificación, en la que se pueden presentar ejemplos visuales, que son de gran utilidad para los alumnos, proporcionando una comprensión más profunda:

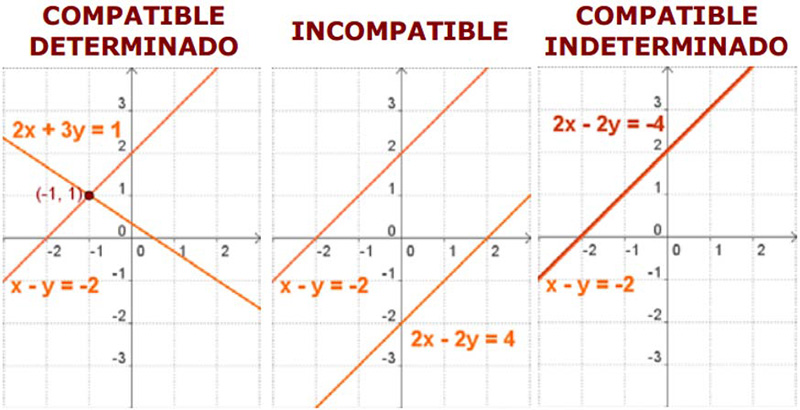
• Sistema Compatible Determinado: El sistema tiene una única solución. Visualmente, se representa como dos rectas que se intersectan en un punto específico, siendo este punto la solución única del sistema.
• Sistema Compatible Indeterminado: El sistema tiene infinitas soluciones. Gráficamente, se refleja mediante dos rectas coincidentes, lo que implica que hay infinitos puntos que cumplen con ambas ecuaciones.
• Sistema Incompatible: Cuando nos enfrentamos a un sistema incompatible, este no tiene solución. En términos visuales, se representa mediante dos rectas paralelas que nunca se cruzan, lo que indica que no hay puntos de intersección, y por lo tanto, ninguna solución posible.

¿Qué opinas de este enfoque organizado para enseñar los métodos de resolución y clasificación de sistemas de ecuaciones lineales? ¿Crees que será útil para tus alumnos? ¡Déjanos tus comentarios y estaremos encantados de leerlos!