¡Qué miedo los desarrollos! No, ¡qué divertidos!

Al final de la etapa Infantil los niños comienzan a aplicar la lógica en sus dibujos y a representar el extenso mundo que van conociendo. Todo es fluido y libre. Sin embargo, al ir enseñando dibujo en cursos más avanzados podemos encontrarnos con alguna dificultad. Existe cierta actitud reacia o temor en los niños cuando ya no pueden dibujar solo libremente, sino que comienzan a utilizar los instrumentos de dibujo como reglas, escuadras, cartabones, el compás, etc. Esto suele suceder cuando se introduce la representación geométrica.

Ahora bien, dicho temor se atenúa si han trabajado de manera sencilla la geometría, junto con las matemáticas, desde la etapa Infantil. En Primaria y Secundaria, nuestra labor es precisamente hacer que asimilen la geometría de forma amena y bonita sin imponer la perfección. No es necesario exigirles niveles que seguramente alcanzarán algún día, pero no en etapas iniciales. Ese miedo que sienten algunas niñas y niños ha de desaparecer y el siguiente ejercicio puede ayudar a ello.

La actividad consiste en que dibujen desarrollos de figuras como el cono, el cilindro o el prisma, los recorten y decoren con grafismos. Básicamente el desarrollo de un sólido es una operación de abatimiento de todas sus caras sobre un único plano a tamaño real. Este ejercicio puede hacerse desde Primaria en adelante, adaptándonos a las distintas edades y habilidades.

Para hacerles comprender, aparte de leer el libro de texto elegido, es recomendable trazar nosotros mismos los desarrollos en la pizarra con tiza. Si hacemos uso directo de la pizarra digital, proyectando imágenes de desarrollos ya resueltos, será insuficiente pues nuestros alumnos no observarán el proceso.

Además, podemos ayudarnos de plantillas que hemos dibujado previamente. Y si estamos enseñando a niños aún pequeños, prepararemos una plantilla que ellos solo tengan que recortar y pegar.

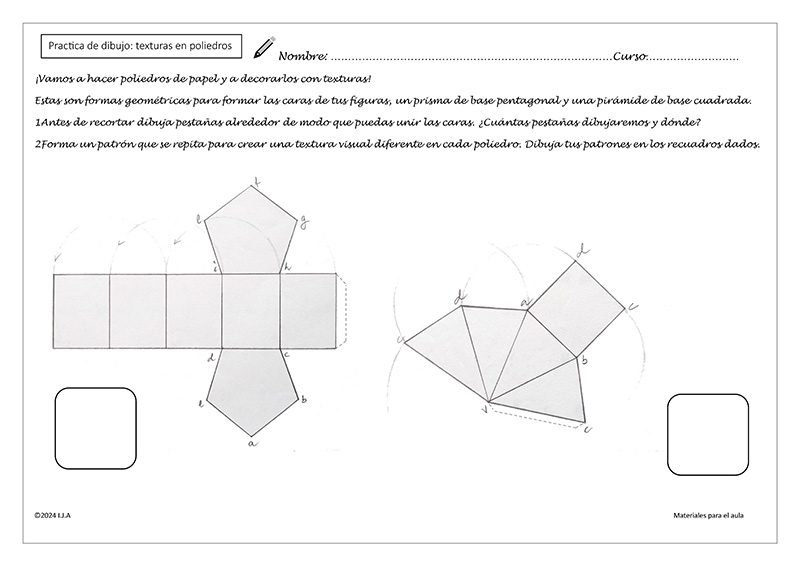
En cursos más avanzados los ejercicios pueden tener un grado más de dificultad, como que nuestros alumnos piensen ellos mismos cómo van a unir las caras del poliedro. Tendrán que discurrir, junto a sus compañeros, dónde dibujar pestañas para recortar y poder pegar. Podéis ver un ejemplo de Plantilla de desarrollos.

Sobre la creación de grafismos hay varios ejercicios que podemos proponer, previamente a trabajar sobre los desarrollos. Básicamente consistirá en elegir un motivo y repetirlo. Tenéis un planteamiento a seguir en el artículo Dibujando, eligiendo y creando.

Una sugerencia es mostrarles algunos ejemplos de diseños de estampados en los que vean claramente la repetición de los motivos. Hay telas muy bonitas que inspirarán a los niños y niñas para crear un grafismo. Este formará una especie de manto que envolverá la figura.

A continuación, resumiré los conocimientos que transmitimos con esta actividad. Aunque son conceptos basados en lo evidente, puede que para ellos sea algo complicado entenderlos. Pero, con lógica y práctica lo irán interiorizando.

• La geometría nos permite comunicar visualmente un mensaje, que es un diseño, y lo hacemos por medio de sistemas. Esto es algo que asimilarán casi sin darse cuenta.
• Un concepto básico que irán comprendiendo es la formación de los planos, sentando las bases para que entiendan la relación entre punto, línea y plano en la geometría elemental plana. Resumidamente, un punto no tiene extensión en el espacio. Una línea, ya sea curva o recta, es un lugar geométrico de infinitos puntos orientados en una única dirección. Y al hablar de plano nos referimos a una superficie plana en la que, si unimos mediante una recta cualesquiera de sus puntos, la recta tiene todos sus puntos en la superficie. Casi podríamos decir que existe poética en la geometría.
• Los poliedros son sólidos limitados por caras planas poligonales. La intersección de las caras define las aristas y, a su vez, la intersección de las aristas determinará los vértices. Pueden ser cóncavos, con ángulo diedro entrante, o convexos, siendo estos últimos los que más se utilizan. Por ejemplo, el hexaedro, el tetraedro o el octaedro que son regulares y pueden inscribirse en una esfera. Lo interesante es que estas figuras, llamadas también superficies, son desarrollables. Es decir, los poliedros se extienden sobre un plano sin deformación de sus elementos.
• Otras figuras como el cono y la pirámide o el cilindro y el prisma son superficies radiadas. Las dos primeras son cónicas, pues se desarrollan en torno a un punto propio. Es decir, las generatrices que van de la base al vértice confluyen en un punto. Y las segundas son cilíndricas porque tienen generatrices que son rectas paralelas. Estas cortan al eje en el infinito, y se  habla entonces de punto impropio.

Para explicar todo esto podemos combinar dibujos en la pizarra, en los que se vean claramente los segmentos que forman las generatrices, con desarrollos en papel o cartulina. Es mejor que estos tengan un tamaño de mediano a grande, y que podamos cerrarlos y abrirlos repetidamente para mostrarlos en clase. Así se darán cuenta de que una superficie es una lámina, no un cuerpo.

En las imágenes podéis ver ejemplos de figuras ya realizadas por alumnos de Secundaria. Obtendremos resultados diferentes en concordancia con, no solo la destreza y habilidad de cada niño sino su imaginación.

Espero que sea de utilidad esta propuesta. Y tú, ¿cómo explicas los desarrollos en tus clases? ¿Te animas a comentarlo?