Indeterminaciones: Guía práctica para profesores de Matemáticas
¿Qué es una indeterminación?
Una indeterminación matemática es una expresión algebraica que aparece en el cálculo de los límites y cuyo resultado no se puede predecir.
Clasificación y Resolución de Indeterminaciones
Existen siete tipos principales de indeterminaciones: cuatro de tipo racional y tres de tipo exponencial. Es crucial recordar que todas las indeterminaciones tienen solución, y se resuelven operando o simplificando los límites hasta llegar a otros equivalentes.
Para resolver cualquier indeterminación, es fundamental ser organizado, metódico y ordenado en la resolución. A continuación, abordaremos cada tipo uno por uno:
Indeterminaciones de tipo racional
- Indeterminación ∞/∞
Esta indeterminación se resuelve dividendo el numerador y el denominador por la potencia de mayor grado. A continuación, se va a presentar un truco muy práctico, que nos puede facilitar mucho la obtención del resultado, de una forma rápida y concisa:
- Si el grado del numerador es mayor que el grado del denominador, entonces el resultado será ±∞, el signo dependerá del coeficiente de mayor grado.
- Si el grado del numerador es igual que el grado del denominador, entonces el resultado del límite será el coeficiente de las potencias de mayor grado.
- Si el grado del numerador es menor que el grado del denominador, entonces el resultado siempre será cero.
- Indeterminación 0/0
Para resolver esta indeterminación, se debe factorizar o multiplicar el numerador y el denominador por el conjugado de la función, en caso de que presente algún radical. Luego, se simplifica la expresión antes de sustituir la variable del límite, eliminando así la indeterminación
- Indeterminación 0*∞
Esta indeterminación se debe transformar en una del tipo ∞/∞ ó 0/0 y se resuelve siguiendo los pasos explicados anteriormente.
- Indeterminación ∞-∞
Esta indeterminación se resuelve operando la expresión dada o multiplicando tanto el numerador como el denominador por el conjugado de la expresión. A continuación, se simplificará la expresión antes de sustituir la variable del límite.
Indeterminaciones de tipo exponencial
Esta indeterminación se resuelve asemejando la expresión dada al número “e”, que se define como:
Una vez que se ha convertido la expresión dada al formato del número “e”, sólo nos quedará resolver el exponente al que estará elevado este número.
Estas indeterminaciones se resuelven tomando logaritmos y aplicando sus propiedades.
Estas indeterminaciones se resuelven tomando logaritmos y aplicando sus propiedades.
Para resolver cualquier indeterminación, es fundamental ser organizado, metódico y ordenado en la resolución
Regla de L’Hôpital
Es importante destacar que las indeterminaciones que surgen del cociente de dos funciones pueden resolverse mediante la regla de L’Hôpital, que consiste en derivar el numerador y el denominador por separado. Esta regla es extremadamente útil y práctica, especialmente cuando los alumnos ya saben derivar.
¿Cómo enfrentan tus alumnos los desafíos de los límites? ¿Qué estrategias has encontrado efectivas para enseñarles a resolver indeterminaciones? ¡Comparte tus técnicas y experiencias con nosotros, y juntos enriqueceremos nuestras prácticas pedagógicas en matemáticas!



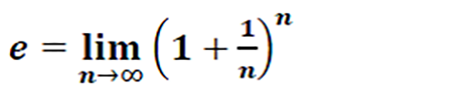



Lo mejor es la regla de L’Hopital, pero hasta que los alumnos aprenden a derivar tienen que usar los otros métodos…
Después de volver a leer el artículo, coincido con la autora en algo que me dijeron hace muchos años: «Las indeterminaciones en los límites matemáticos pueden convertirse en un verdadero desafío para los estudiantes si no las comprenden bien.» Debo añadir que lo que nos proporciona la autora no me parecen «trucos». Enhorabuena y gracias.
Muy bueno, muchas gracias
Siempre se me han atragantado las intederminaciones exponenciales. Creo que si no se tiene una buena base en matemáticas, en mi caso aplicando los logaritmos y sus propiedades, no se entienden conceptos mas avanzados. Qué importante es el entendimiento de las matemáticas desde pequeños para poder luego entender conceptos mas avanzados.