¿Qué significa dividir en la metodología Singapur?
Las “matemáticas Singapur” o, quizá de manera más apropiada, la “metodología Singapur para la enseñanza de las matemáticas”, viene precedida de un gran éxito a nivel internacional, desde que hace ya 30 años se implantara en el país que le ha dado nombre. SM recoge este aprendizaje en su proyecto Piensa infinito dirigido a los alumnos de Primaria.
El Dr. Yeap Ban Har, referente internacional en la metodología que encabeza los resultados de PISA y TIMSS, es el autor y supervisor de la solución educativa de SM Piensa infinito, adaptando esta nueva manera de aprender matemáticas al currículo de España.
Pedro Ramos, profesor de Matemática Aplicada de la Universidad de Alcalá, nos da unas pistas y ejemplifica este novedoso método.
El foco consiste en que los alumnos comprendan lo que están haciendo cuando usan un símbolo matemático, o cuando realizan una operación; que sepan razonar y que puedan aplicar sus conocimientos a la resolución de problemas.
Este aprendizaje se consigue introduciendo los diferentes conceptos a través de situaciones, de manera que los niños tengan oportunidad de darles sentido. Para ello se utilizan materiales manipulativos específicamente diseñados para conseguir un buen aprendizaje (fase concreta) y se representa gráficamente la información (fase pictórica). Posteriormente, se pasa a la fase abstracta, donde se formalizan las estrategias previamente desarrolladas y se consigue un aprendizaje basado en la comprensión.
En muchas aulas se oye que “dividir es repartir”, y eso no es siempre así. Para verlo vamos a considerar estas dos situaciones:
- Luisa tiene 20 pegatinas y quiere repartirlas (por igual) entre sus cuatro amigos. ¿Cuántas pegatinas le tocan a cada uno de sus amigos?
- Carlos tiene 20 caramelos, y quiere hacer bolsas de cuatro caramelos. ¿Cuántas bolsas puede hacer?
Desde el punto de vista de la división, las dos preguntas se pueden contestar haciendo la misma operación: 20 : 4 = 5. Sin embargo, el significado de estas dos divisiones no es el mismo. Una forma de ver esto es pensar en cómo resolvería estos problemas un alumno que está empezando Primaria, y que no ha oído hablar de la división. En el primer caso, empezaría a repartir pegatinas por rondas, de una en una, hasta ver que cuando termina la quinta ronda se ha quedado sin pegatinas, y, por tanto, le ha dado a cada amigo 5 pegatinas. En el segundo caso, haría grupos de 4 caramelos, y vería que después de completar el quinto grupo ha terminado, y tiene, por tanto, 5 bolsas de caramelos.
Otra forma de comprobar la diferencia entre las dos situaciones es verbalizar la operación y su relación con la multiplicación en términos de grupos.
En el caso (a), tenemos 20 pegatinas, y Luisa quiere hacer 4 grupos iguales, para darle un grupo a cada amigo. La división nos dice que cada grupo tendrá 5 pegatinas. Por tanto, 20 : 4 = 5, porque 4 grupos de 5 son 20.
En el caso (b), tenemos 20 caramelos, y queremos hacer grupos con 4 caramelos. La división nos dice que podremos hacer 5 grupos. Por tanto, 20 : 4 = 5, porque 5 grupos de 4 son 20.
Por supuesto, las dos frases finales son multiplicaciones cuyo resultado es el mismo por la conocida propiedad conmutativa, pero el significado es diferente.
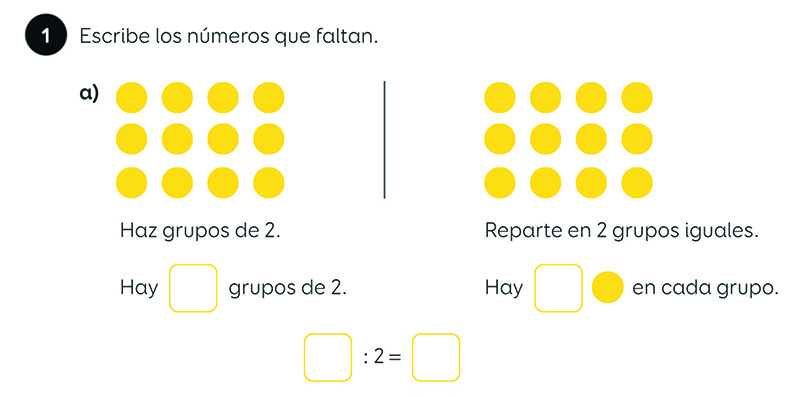
Vamos a ver un ejercicio, tomado directamente del libro de 2º de Primaria de Piensa infinito, de SM, para terminar de comprender estos dos significados de la división. Animamos al lector a que olvide por un momento los cálculos de divisiones, y a que intente hacer el ejercicio dibujando, como lo haría un alumno de 2º de Primaria que está empezando a trabajar la división. Solo al final resumimos la situación, escribiendo la representación simbólica de las divisiones que hemos obtenido dibujando (la representación simbólica es la misma en los dos casos).
El primer significado de la división es el conocido «repartir»; el siguiente se suele conocer como «agrupar». Una variante de este segundo significado aparece con frecuencia en contextos de medida: si tenemos una colección de libros de un grosor de 8 cm y una estantería de 60 cm, ¿cuántos libros podré colocar en la estantería? La respuesta nos la da, de nuevo, el cociente de la división 60 : 8, que nos dice cuántas veces «cabe» 8 en 60.
Por alguna razón, este segundo significado no se suele trabajar de manera sistemática en la enseñanza tradicional de las matemáticas en España, y esto puede ser fuente de dificultades en la resolución de problemas cuando llegamos a cursos más avanzados. Las dificultades se perciben de manera muy clara cuando se llega al estudio de las fracciones.
Consideremos la siguiente operación: 4 : 2/3. ¿Puede el lector darle significado? Dicho de otra forma, ¿puede pensar en un problema, o una pregunta, en el que para llegar a la respuesta se necesite hacer este cálculo?
La única forma de comprender las matemáticas es realizar tareas que requieran reflexión.
Más en thrivu.grupo-sm.com
Para saber más sobre esta metodología y otras, puedes entrar en Thrivu y descargar algunos retos para el aula. ¡Anímate!
Thrivu es la comunidad educativa de SM donde encontrar recursos, descargables, actualidad educativa, webinars… Un lugar donde ofrecer a los profesores aquello que les aporte de verdad. Un espacio vivo y práctico donde ayudarte a seguir creciendo. Porque somos lo que construimos entre todos.


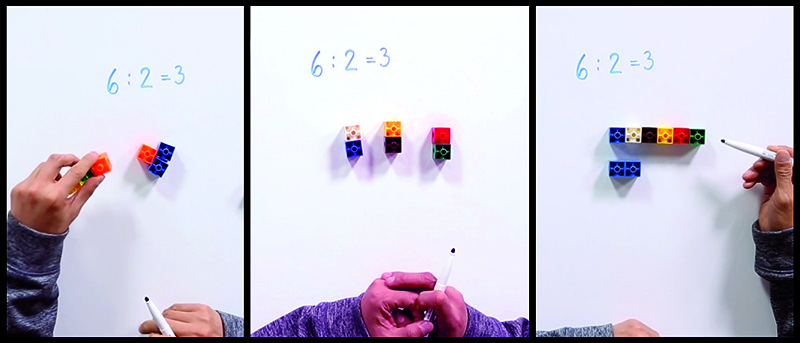

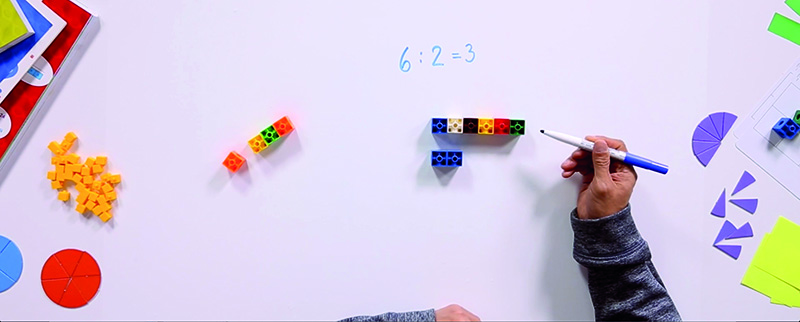
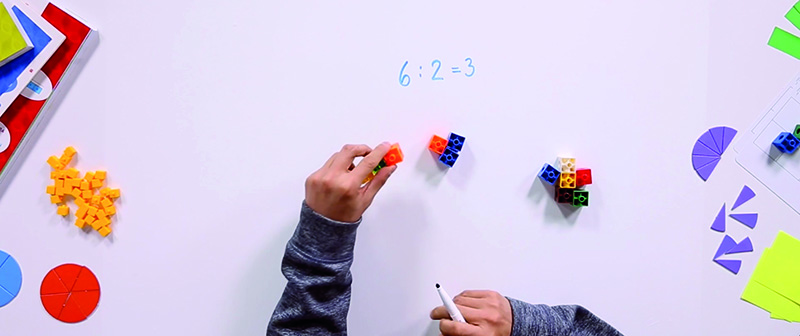
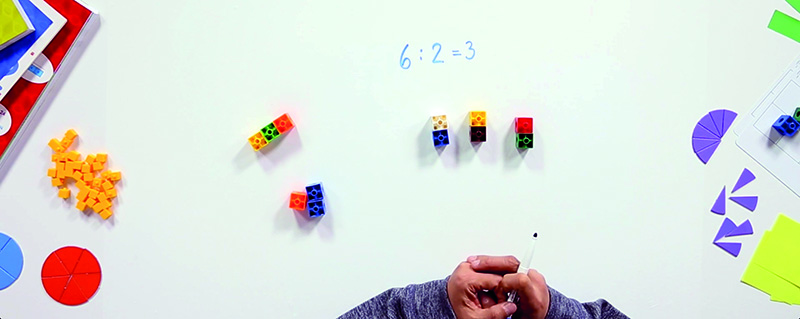
[…] ¿Qué significa dividir en la metodología Singapur? […]