Descifrando el poder de la matriz inversa
Definición y Condiciones para la Existencia:
La matriz inversa, representada por A¯¹, es aquella que cumple que AA¯¹= A¯¹A=I, es decir, que la matriz A multiplicada por la matriz Identidad resulta ella misma.
¿Todas las matrices tienen matriz inversa? La respuesta es no. Sólo aquellas que cumplan:
- La matriz es cuadrada: mismo número de filas que de columnas
- El determinante de la matriz sea distinto de cero, lo que se conoce como matriz regular.
Se han de cumplir estas dos condiciones para afirmar que existe matriz inversa, en cuyo caso se puede definir la matriz original como matriz regular. Antes de enfrascarse en un método para calcular la Matriz Inversa, siempre se recomienda comprobar si se cumplen estas dos condiciones.
Características de la matriz inversa:
- Es única.
- La inversa de la matriz inversa es la matriz original.
- El producto de la inversa de dos matrices es la inversa de la segunda matriz por la inversa de la primera matriz.
- La inversa de la matriz traspuesta es la traspuesta de la matriz inversa.
- El determinante de la matriz inversa es la inversa del determinante de la matriz original.
Formas de calcular la matriz inversa:
1. Por la propiedad de la matriz inversa
Fijándonos en la propia definición, AA¯¹=I, se puede calcular directamente. Es decir, para una matriz cualquier orden, se realiza la multiplicación de matrices y se obtienen los elementos de la matriz inversa.
2. Método de Gauss – Jordan
Este método consiste en poner la matriz que queremos invertir seguida de la matriz identidad del mismo orden, separadas por una línea recta vertical: (A│I) →(I│ A¯¹) y transformar la primera en la identidad con combinaciones elementales entre sus filas. La matriz inversa será la matriz obtenida a la derecha de la línea recta. ¡Ojo! Si al hacer las transformaciones ocurre que en la parte izquierda hay una fila entera de ceros es porque no existe matriz inversa.
Las transformaciones que se pueden aplicar serían:
- Cambiar el orden de las filas.
- Multiplicar o dividir todos los elementos de una fila.
- Sustituir una fila por la suma de su misma fila más otra multiplicada por un número.
3. Método de los adjuntos
Este método se basa en la fórmula:
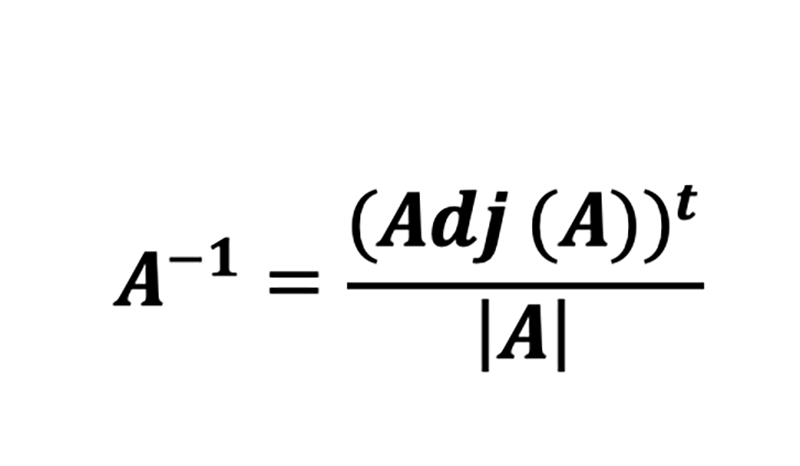
- Donde el adjunto de la matriz A se calcula mediante la matriz de cofactores y su transpuesta.
- Método muy útil para matrices de orden superior.
Siempre es muy útil conocer los tres, ya que a veces uno no consigue llegar al resultado por un método y decide emplear otro, o bien porque quiere hacer una comprobación confirmando que ha llegado a la solución correcta probando otro método. Puede ser que un método guste más que otros, es cuestión de entenderlos, practicarlos y elegir el que más guste.
Aplicaciones de la matriz inversa
La matriz inversa, aunque puede parecer compleja al principio, se convierte en una herramienta valiosa en diferentes contextos matemáticos, como la resolución de sistemas de ecuaciones matriciales. Siendo un sistema:
AX=B, para despejar la matriz X, habrá que seguir los siguientes pasos:
Multiplicar a ambos lados de la igualdad por la inversa de la matriz A: A¯¹ AX= A¯¹ B,
Sabiendo que A¯¹ A=I, entonces la matriz incógnita sería X= A¯¹ B.
¿Conocías estos tres métodos para calcular la matriz inversa? ¿Cuál te parece más sencillo de utilizar? ¡Escríbenos en comentarios y aprenderemos de tu experiencia!



Gracias, buenísima explicación!!
Muy útil y bien explicado un tema que cuesta mucho hacer entender a los alumnos. Fundamental que lo entiendan de cara a su futuro universitario con la asignatura de Algebra
Muy clara y sencilla, la explicación de la matriz inversa. Enhorabuena a la autora!!!
Qué buen artículo, se explica lo que es la matriz inversa además de los métodos para calcularla y sus aplicaciones. Sin duda, ayudará a muchos alumnos de cara a la EVAU.
Enhorabuena! Mucho mérito simplificar la complejidad de los tres métodos. Súper útil.
Es una descripción de la matriz inversa concreta, concisa y, al mismo tiempo, completa, sencilla y muy útil.
Muy buen trabajo.
Hasta yo, que soy de letras, he entendido lo que es una matriz inversa, los métodos para calcularla y sus aplicaciones, pero no me atrevería a explicar ninguno de esos tres conocimientos, si no es con el artículo en la mano. Gracias, por el esfuerzo de explicarlo con esa claridad.