De principiantes a expertos: cómo resolver ecuaciones con confianza
Las ecuaciones polinómicas son familiares para los alumnos y se dividen en varios tipos según el grado de la incógnita:
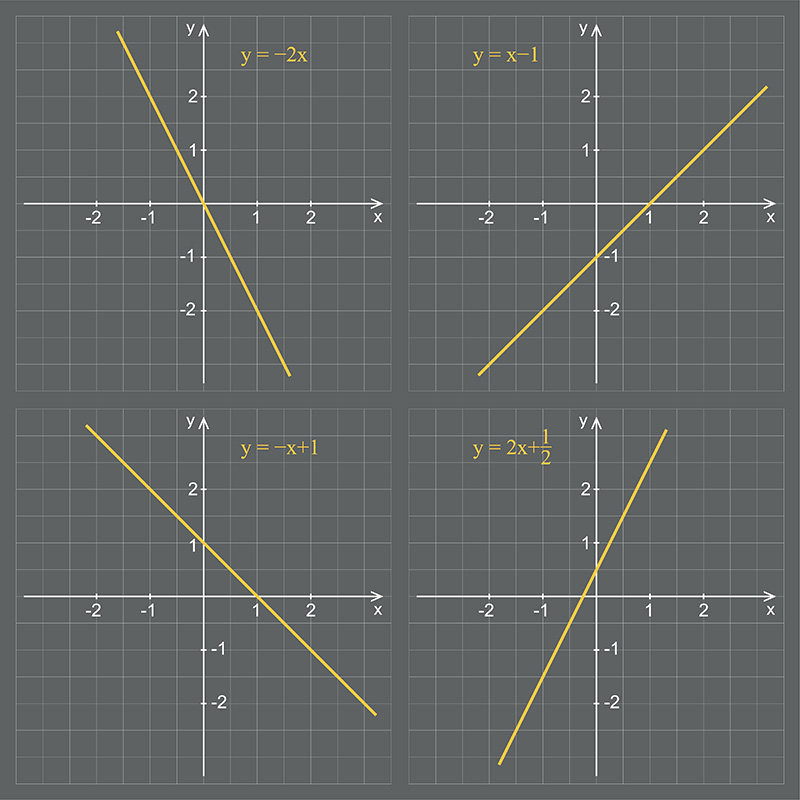
Primer grado
Ecuaciones del tipo ax+b=0, se resuelven fácilmente despejando la incógnita “x”.
Segundo grado
Ecuaciones del tipo ax²+bx+c=0, se resuelven utilizando la fórmula:

Grado mayor que dos
Se resuelven mediante Ruffini.
Ecuaciones bicuadradas

Se resuelven mediante un cambio de variable (x²=t)
Son ecuaciones del tipo 1/x
- Calcula el Mínimo Común Múltiplo (m.c.m.) para eliminar la incógnita de los denominadores.
- Resuelve la ecuación despejando la “X”.
- Asegúrate de que ninguna de las soluciones anule los denominadores.
Son ecuaciones del tipo √x
- Aísla la raíz en un miembro de la igualdad.
- Eleva al cuadrado ambos lados de la ecuación.
- Resuelve la ecuación resultante.
- Verifica que las soluciones no generen raíces negativas y cumplan con la ecuación original. Recuerda repetir los pasos 1 y 2 si hay más de una raíz, hasta eliminarlas por completo.
Son ecuaciones del tipo log x
- Utiliza las propiedades o la definición de logaritmo:
-Definición:
![]()
-Propiedades:

- Resuelve la ecuación resultante.
- Comprueba que las soluciones obtenidas no generen logaritmos negativos y cumplan con la ecuación original.
Son ecuaciones tipo del tipo
![]()
Existen varias opciones para resolverlas:
Opción 1
Expresa la ecuación como potencias de la misma base.
Opción 2
Realiza un cambio de variable
![]()
Si ninguna de las opciones anteriores es viable, toma logaritmos en ambos lados de la igualdad.
Estos consejos prácticos proporcionan un enfoque estructurado para abordar distintos tipos de ecuaciones. ¿Qué te parecen? ¡Déjanos tus comentarios y estaremos encantados de leerte!





Qué bien resumido está!!!!!!!!! Muchas gracias por facilitarnos la vida a los docentes. Con este resumen tan bien estructurado no van a tener dudas a la hora de resolver una ecuación.
Muy buenos consejos, muy acertados y con un enfoque bien estructurado. Gracias por el artículo
Buena técnica para que los alumnos adquieran confianza y afronten con seguridad las ecuaciones.
No cabe duda que esta autora tiene el don de la claridad y de hacer fáciles y «simpáticas» las matemáticas. Gracias.
Coincido con Pilar. Una pregunta: ¿La simpática señorita que aparece al principio es la imagen de la autora?
Ay si hubieramos tenido este resumen antes del examen!!!!! Para la siguiente evaluación me lo apunto. Muchas gracias por sintetizar tan bien la materia.
Así explicado, parecen hasta divertidas las ecuaciones. Están muy bien estructurados y resumidos los procedimientos a seguir. Un saludo
Llevo siguiendo tu trayectoria desde que empezaste. Me parece que explicas muy bien y tus art8culos son muy útiles a mis alumnnos.
Útil como resumen a trasladar a los alumnos. No obstante hay que complementarlo con ejercicios prácticos donde pongan cada método en uso
El tema lo has dejado, sencillo y claro, ahora, a ver si los alumnos lo asimilan con facilidad. Gracias por el artículo.
Con este artículo, se ayuda a reforzar el aprendizaje de las ecuaciones y ayudar a los alumnos a que vean la importancia que tienen en el mundo real, ya que las ecuaciones son fundamentales en matemáticas y además, se pueden aplicar en distintas áreas.