Cómo trabajar la continuidad de funciones: Una guía práctica para estudiantes
Una función es continua cuando, al dibujarla, no necesitamos levantar el lápiz del papel. © EDUARDO LEOPOLDO
Para entender la continuidad, comenzaremos con una idea muy simple: dibujemos una función explicando que una función es continua cuando, al dibujarla, no necesitamos levantar el lápiz del papel. Aunque esta definición es bastante básica, es una excelente manera de empezar a familiarizarse con el concepto.
Una vez que esta idea esté clara, avanzaremos hacia una definición más precisa: Una función es continua en un punto, x=a, cuando el valor de la función en ese punto es igual al límite de la función en ese mismo punto:
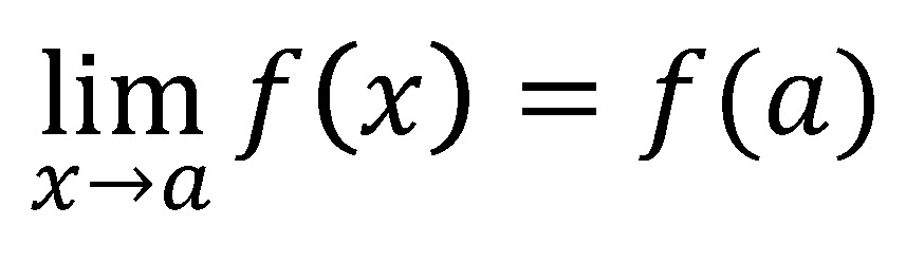
Luego, examinaremos lo que ocurre cuando la función NO es continua en ese punto. Primero, identificaremos los puntos donde puede haber discontinuidades, es decir, donde la función no está definida. Estos puntos pueden incluir:
- Puntos que anulan el denominador de una función racional.
- Puntos que resultan en una raíz cuadrada negativa.
- Puntos que dan como resultado un logaritmo neperiano o decimal menor o igual que cero.
- En funciones a trozos, los extremos de cada intervalo, donde la función puede cambiar.
Aquí es donde se presentan los diferentes escenarios de discontinuidades:
1. Discontinuidad evitable
Ocurre cuando el límite de la función en el punto de posible discontinuidad presenta un valor finito, pero diferente al valor que toma la función en ese punto. Veamos matemáticamente cómo se calcularía:
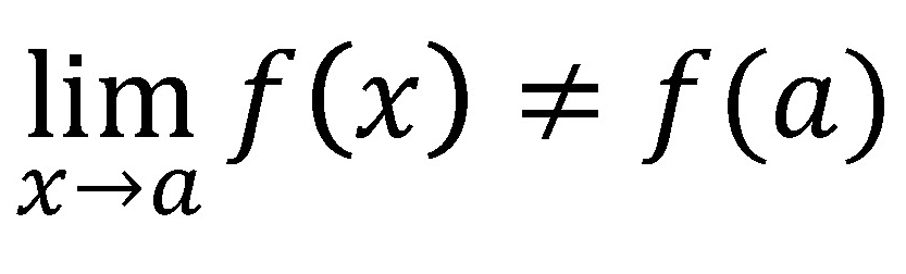
2. Discontinuidad inevitable
En este caso, la discontinuidad puede ser de dos tipos:
Salto finito. Se calcula mediante los límites laterales (límite a izquierda y derecha del punto de posible discontinuidad). Los resultados son números finitos, pero de diferente valor.
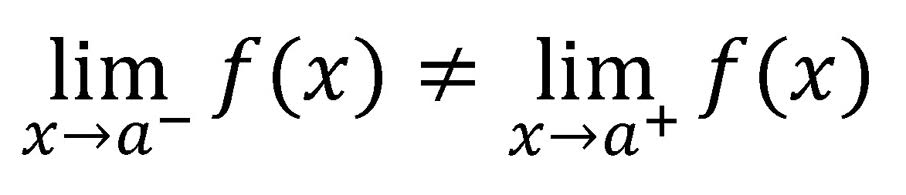
Salto infinito. Similar al salto finito. Pero uno o ambos límites laterales son infinito.
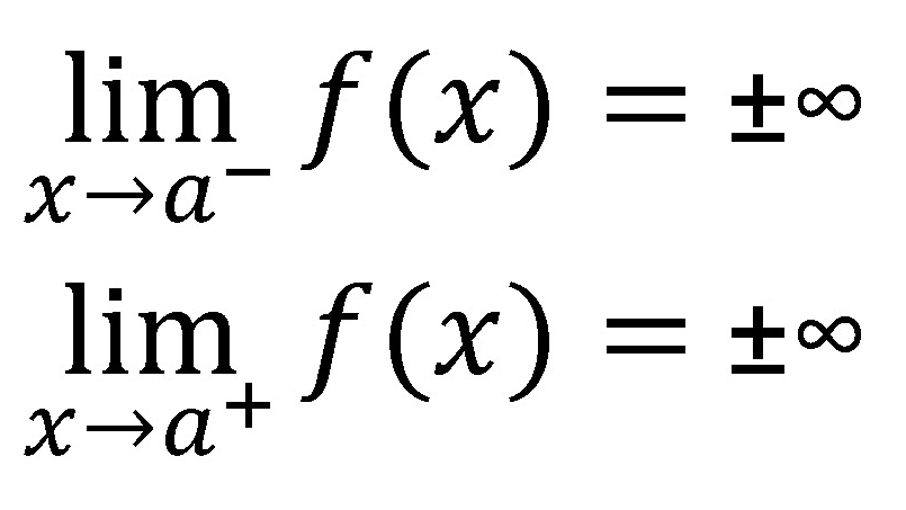
Es muy aconsejable dibujar una gráfica para cada tipo de discontinuidad, permitiendo a los estudiantes visualizar y entender cada caso, su significado y sus implicaciones. Por supuesto, la mejor manera de internalizar esta teoría es practicando con ejemplos concretos.
¿Cuál ha sido tu experiencia al enseñar estos conceptos en clase? ¿Tus estudiantes logran comprender bien estos principios? ¡Comparte tus experiencias y juntos seguiremos creciendo en esta apasionante tarea educativa!






Creo que por fin acabo de entender este tema que siempre me da dolores de cabeza. Gracias por explicarlo tan bien.
Los artículos de esta autora nunca defraudan. Muchas gracias por hacernos llegar a todos las matemáticas
Con pequeñas cosas que memorizar, lo que se puede aprender de una funcion!
Muy bien explicado: breve y conciso.
La continuidad de las funciones es un concepto fundamental en matemáticas, porque nos permite comprender mejor el comportamiento de las funciones y suavizar cualquier irregularidad en sus gráficas.
Reconozco que siempre me ha costado entender este tema, pero aquí leyéndolo me parece que hasta lo he entendido. Muchas gracias por la explicación!
Muy bueno, gracias!
Acabo de leer el artículo y desde luego que sirve de guía práctica, sencilla y fácil para los alumnos. Gracias por explicarlo así de bien.