Polinomios: Qué son y para qué sirven
Los polinomios pueden emplearse por ejemplo para analizar las pérdidas y ganancias de una empresa. © WHO IS DANNY
¿Qué es un Polinomio?
Un polinomio es una expresión algebraica compuesta por la suma o diferencia de varios monomios.
Su expresión matemática es:
Siendo el grado del polinomio el exponente del término de mayor grado.
Ejemplo: indicar el grado del siguiente polinomio:
Las raíces de un polinomio son los valores de “a” para los que el valor numérico del polinomio sea cero. Matemáticamente hablando, se podría decir: x=a es una raíz de P(x).
Operaciones con polinomios
Suma y resta
Para sumar o restar polinomios, se suman o restan los términos de igual grado.
Multiplicación
Multiplicar un polinomio por un número no nulo da como resultado un polinomio del mismo grado, cuyos coeficientes son los del polinomio inicial multiplicados por ese número.
Ejemplo: Multiplicar el siguiente polinomio por 2, P(x)=x²-x-1
El resultado sería:
P(x)=2x²-2x-2
El producto de dos polinomios se obtiene aplicando la propiedad distributiva, multiplicando cada término del primer polinomio por cada término del segundo.
División
Dos polinomios pueden dividirse cuando el grado del dividendo es mayor o igual que el grado del divisor. Para la división, se puede utilizar la Regla de Ruffini.
Factorización de polinomios
Factorizar polinomios es escribirlos como producto de polinomios de menor grado posible.
Teorema del resto
El valor numérico de un polinomio P(x) para x=a coincide con el resto que se obtiene al dividir P(x) por (x-a), es decir, R=P(a).
Teorema del Factor
Si x=a es una raíz del polinomio P(x), (x-a) es un factor de P(x).
P(a)=0, es decir, P(x)= (x-a)Q(x)
Ejemplo: Comprobar si (x-2) es un factor del polinomio P(x)=x³+5x²-4x-20.
Se sustituye x=2 en el polinomio P(x=2) = 2³ + 5 · 2² – 4 · 2 – 20= 0, por lo tanto, se puede afirmar que (x-2) es un factor del polinomio.
Métodos de Factorización
Existen varios métodos para factorizar polinomios:
- Extracción de factor común
- Uso de identidades notables
- Regla de Ruffini y Teorema del Resto para hallar las raíces del polinomio
- Resolución de ecuaciones de segundo grado para polinomios de grado 2
Recursos digitales
Hoy en día, existen herramientas digitales que facilitan la factorización de polinomios. Una de las más recomendadas es Symbolab, una potente herramienta que resuelve ecuaciones matemáticas, desde integrales y límites hasta, en este caso concreto, la factorización de polinomios.
¿Qué tal se desenvuelven tus alumnos con los polinomios? ¡Déjanos tus comentarios y juntos descubriremos los misterios de la factorización de polinomios!



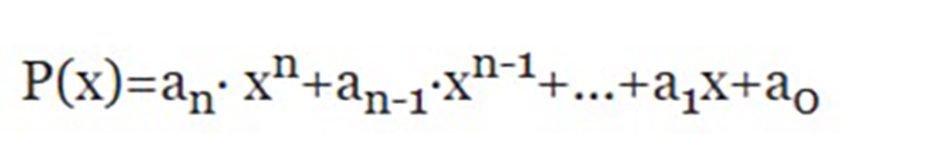





Me encanta lo bien que sintetizas los conceptos, haces que se entienda todo de una manera clara y sencilla. Me ha gustado mucho el artículo.
Coincido con Inés: acertada síntesis de los conceptos y explicados con una claridad y sencillez envidiables. Pienso que por su interés, aplicabilidad y ayuda a la formación del pensamiento matemático, merecería seguir con este tema.
Transmites de forma clara y sencilla el concepto de polinomio y la factorización del mismo. Gracias por la estructura del artículo, pues una buena síntesis.
Los polinomios son muy útiles para fomentar las habilidades analíticas: ayudan a descomponer problemas complejos en partes más manejables. También ayudan al desarrollo del pensamiento lógico y la resolución de problemas.
Para analizar datos, los polinomios son una buena herramienta, además de la asignatura de matemáticas, se utilizan en informática, física, ingeniería y economía. Es importante trabajarlos bien en el aula, para que los alumnos adquieran correctamente el concepto de polinomio.
Los polinomios ayudan a tener una buena base para el cálculo, el álgebra lineal y la teoría de números.