Domina la técnica de la integral por partes con estos consejos infalibles
¿Cómo identificar una integral por partes?
El primer paso para abordar una integral por partes es identificar si estamos realmente ante este tipo de integral. Generalmente, la clave está en observar un producto dentro de la integral. A diferencia de las integrales inmediatas, donde la función se integra directamente, en las integrales por partes nos encontramos con una expresión que es el producto de dos funciones distintas, y es aquí donde aplicamos la fórmula de integración por partes:
La fórmula de la integral por partes es la siguiente:
Esta fórmula puede parecer intimidante al principio, pero con la práctica se convierte en una herramienta poderosa. Una forma sencilla de memorizarla es utilizando una regla nemotécnica, como “Un Día Vi Un Valiente soldadito Vestido De Uniforme”, donde las iniciales de cada palabra nos recuerdan las letras clave de la fórmula: u, v, du y dv.
La regla ALPES
Uno de los aspectos más críticos en la resolución de integrales por partes es la correcta selección de las funciones u, v, du y dv. La elección adecuada de estas funciones puede simplificar enormemente la integral restante, mientras que una mala elección puede complicarla. Para ayudarte en esta decisión, existe una regla nemotécnica conocida como ALPES, que prioriza el tipo de función que deberías elegir como u en función de la siguiente jerarquía:
- Arco- (arco seno, arco coseno, arco tangente)
- Logaritmo
- Potencia
- Exponencial
- Seno/coseno
Si en la integral aparece una sola de estas funciones, esa debería ser tu función u, mientras que dv sería simplemente el diferencial dx. Pero ¿Qué pasa si tienes más de una de estas funciones? Aquí es donde la regla ALPES muestra su utilidad: debes escoger como u la función que aparezca primero en esta lista, y la otra función, junto con dx, será dv.
Profundizando en la técnica: ejemplo práctico
Veamos cómo se aplica esta técnica con un ejemplo concreto:
En este caso, la integral involucra un producto de dos funciones: , que es una potencia, y , que es un logaritmo. Sabemos que no podemos resolver esta integral de manera directa, lo que nos lleva a identificarla como una integral por partes. Aplicando la regla ALPES, el logaritmo aparece antes que la potencia, por lo que:
A continuación, derivamos u para obtener du, e integramos dv para obtener v:
Ahora podemos aplicar la fórmula de la integral por partes:
Al simplificar la integral restante, observamos que se convierte en una integral inmediata, lo que facilita obtener el resultado final. Este enfoque paso a paso no solo te ayudará a resolver la integral específica, sino que también te proporcionará una estructura para abordar integrales similares en el futuro.
La integral por partes es una técnica poderosa que, cuando se domina, abre la puerta a resolver integrales más complejas. ¿Cómo ha sido tu experiencia enseñando o aprendiendo esta técnica? ¿Tus alumnos la han entendido bien? ¡Nos encantaría conocer las reglas y enfoques que has utilizado para facilitar la comprensión de las integrales por partes! Comparte tus experiencias y ayuda a otros a dominar esta herramienta esencial en el cálculo.



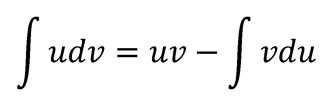
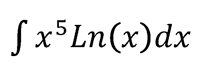

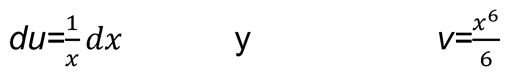
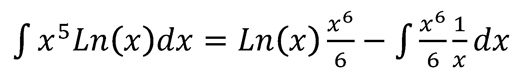



Tengo que volver a leer el artículo, pero, me parece, que los consejos y estrategias para identificar y resolver integrales por partes, son acertados y bastante fáciles de seguir. Enhorabuena y una vez más mis felicitaciones a la autora.
La primera regla nemotécnica la conocía, pero la regla de los ALPES no, me parece una idea genial para que los alumnos no se equivoquen!!!! Muchas gracias por las ideas
Buenísimo artículo!!!!!! Las integrales por partes son un básico en el currículum matemático. Muy bien explicado y muchas gracias por los ejemplos, se entiende muy bien.
No veo las fórmulas. Es una pena porque sin ellas no acabo de entender el artículo.
Yo tampoco veo las fórmulas. Es una pena
Me pasa lo mismo
Me parece una explicación clara y sencilla, además aportas dos reglas nemotécnicas para aplicar en las integrales por partes, que «suavizan» el primer momento de enfrentarse a ellas
Cualquiera de los dos técnicas son efectivas para obtener una integral más sencilla que la original. Estas integrales son relevantes también en aplicaciones de la ingenieria y científicas. Son fundamentales para resolver problemas de física y de estadística.
El artículo es muy interesante y muy útil. Pero no consigo ver las fórmulas…así que no veo el ejemplo práctico
Este artículo no puede ser más útil: claro, conciso, sencillo, práctico, bien explicado y muy bien explicado
Creo que después de mucho tiempo he entendido como se calculan las integrales por partes. Muchas gracias
No consigo ver las fórmulas ni el ejemplo concreto, he probado en windows y en ios y nada