Técnicas para explicar y entender el proceso de Racionalizar
Racionalizar es eliminar las raíces del denominador de una fracción. Lo que nos permite expresar los resultados de una forma más “limpia”, facilitando la comprensión y uso de los números en cálculos posteriores. Aunque en algunas situaciones no afecta directamente, racionalizar simplifica los cálculos haciéndolos más manejables. En muchos problemas algebraicos, físicos e incluso geométricos, la racionalización ayuda a evitar errores y a obtener resultados más claros.
A continuación, veremos tres situaciones comunes que se nos presentan y cómo resolverlas de manera sencilla, para que puedas llevar estas ideas al aula con confianza.
1. Cuando hay una raíz cuadrada en el denominador
Este es el caso más común. Si en el denominador tenemos una raíz cuadrada, la solución pasa por multiplicar tanto el numerador como el denominador por la misma raíz. De este modo, aprovechamos que una raíz cuadrada elevada al cuadrado elimina la raíz.
Ejemplo:
Ahora, la raíz ha desaparecido del denominador, ¡misión cumplida!
2. Cuando el índice de la raíz no es 2
Si el radical en el denominador tiene un índice distinto de dos, debemos elevar ese radical a la diferencia entre el índice de la raíz y el exponente del radicando para que la raíz se elimine.
Ejemplo:
¡Listo! El denominador ya no tiene raíz.
3. Cuando hay una suma o diferencia de raíces en el denominador
Este caso es algo más complejo, pero muy frecuente en el aula. Si encontramos una suma o diferencia de raíces, necesitamos multiplicar por el conjugado del denominador. El conjugado es simplemente el mismo término, pero con el signo opuesto. Esto permite tener en el denominador la identidad notable de la diferencia de los cuadrados, para así poder eliminar las raíces.
Ejemplo:
La raíz ha desaparecido del denominador y hemos logrado un resultado simplificado.
Este tipo de racionalización es más avanzado, y puede ser una oportunidad para introducir a los estudiantes al concepto de los conjugados y su importancia en diferentes ramas de las matemáticas, como en el cálculo de números complejos. Entender este paso no solo ayuda a racionalizar fracciones, sino que abre las puertas a conceptos más amplios.
Una vez que los estudiantes comprenden cómo racionalizar, es importante hacer conexiones con otros temas de matemáticas. Por ejemplo, la racionalización aparece en la simplificación de expresiones algebraicas, en la resolución de ecuaciones irracionales y hasta en la trigonometría cuando trabajamos con identidades. Mostrar cómo la técnica se entrelaza con diferentes áreas les dará a los estudiantes un sentido de unidad y continuidad en las matemáticas.
Ahora que hemos explorado estas técnicas, es tu turno. ¿Cómo abordas la racionalización en tus clases? ¿Tienes algún truco o enfoque creativo que funcione especialmente bien con tus alumnos? ¡Compártelo en los comentarios y sigamos creciendo juntos en el maravilloso mundo de las matemáticas!
Accede a una calculadora para racionalizar aquí.



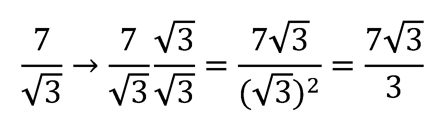
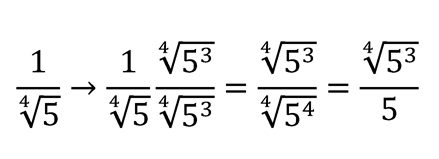
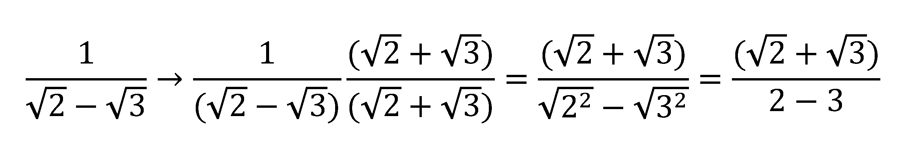



Super claro y bien explicado. Me encanta la última situación, porque entran en juego identidades notables y se aprende a relacionar conceptos matemáticos. Enhorabuena a la autora!
«Trucos» útiles, sencillos y eficaces. Todo alumno debe conocerlos.
No puedo ver los ejemplos, no se descargan.
magisnet.com, yo tampoco puedover los ejemplos
Muy bien explicado el tercer supuesto: el de los conjugados.
Los ejemplos no se ven, ni en Android, ni en IOS.
La forma que propones para explicarlo a los alumnos es muy atractiva y «estimulante»